Virus symmetry and T number

Caspar-Klug Theory

The Caspar-Klug Theory (CK Theory) is built upon 60 identical subunits organized on the 20 triangles creating the faces of an icosahedron. These icosahedral structures exhibit rotational symmetry: 5-fold symmetry at the vertices, 2-fold through the edges and 3-fold through the center of each triangular face. Each triangular facet can be divided into three symmetrically equivalent parts, called an icosahedral asymmetric unit (IAU), by the 3-fold symmetry axis.

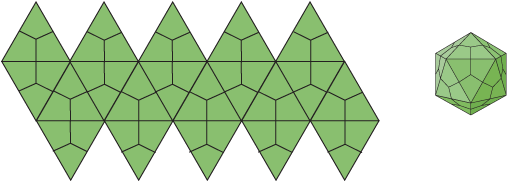
T-number.

The CK Theory enumerates the possible designs for icosahedral surface lattices by mapping the unfolded 20 triangular faces of an icosahedron onto a two dimensional hexagonal lattice. It is assumed this lattice consists entirely of regular hexagons, with the exception of each vertex from the triangulation should be a pentagon. These pentagons curve the hexagonal matrice into a sphere. The triangulation number (T-number) is mathematically defined as the squared length of each triangle edge. It counts the number of symmetrically distinct but quasi-equivalent triangular facets in the triangulation per face of icosahedron.

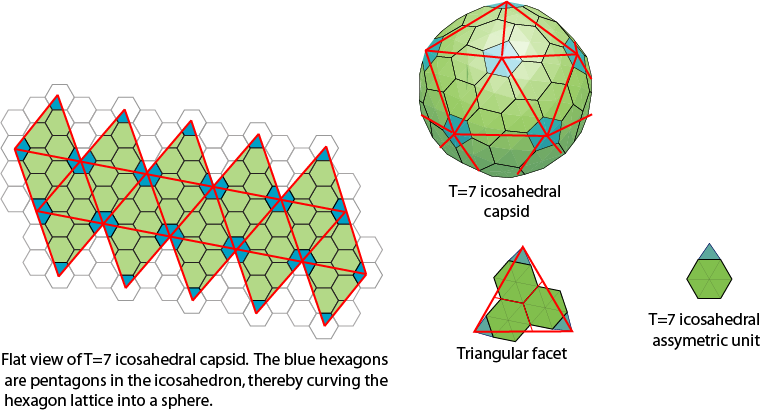
T numbers in ViralZone:

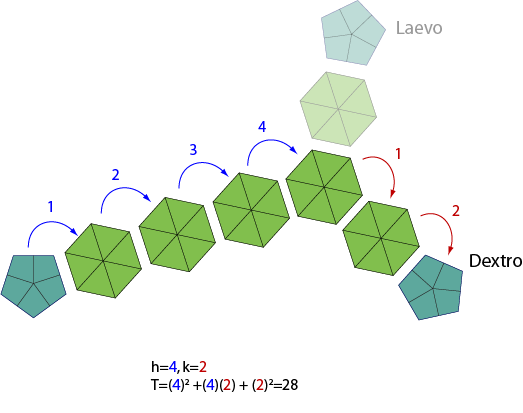
By simplification ViralZone displays the formula: T= h<sup>2+hk+k<sup>2 where h and k are nonnegative numbers. h is the number of units in straight line toward next pentagone, k is the number of units shifted in either side to reach the next pentagon.

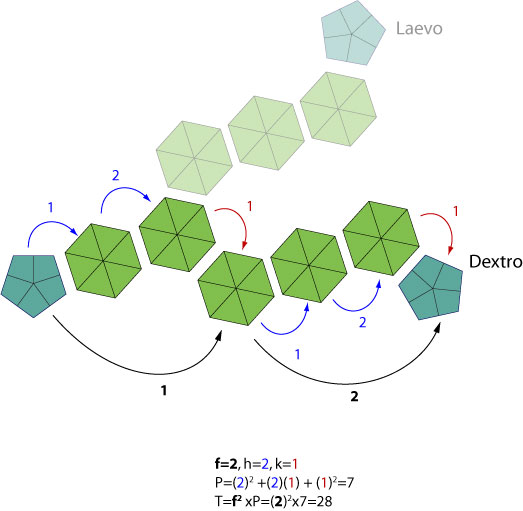
The Original Caspar-Klug formula:

T= F*(h<sup>2+hk+k<sup>2) where h and k are nonnegative numbers representing identical pattern forming the face, and F the number of times this pattern is repeated. h is the number of units in straight line toward next pentagone, k is the number of units shifted in either side to reach the next pentagon.